链式前向星

众所周知，存图的方式有多种，例如邻接矩阵，邻接表，这两种一般初学者都在用，并且十分的便于理解和使用。但是当图的边数过大或者说点数较大时以上两种存图方式不是十分的合适。

所以说，这时就要用到我们的链式前向星了。本质上来说是用链表实现的临接表，先放代码。

    int e[N],w[N],ne[N],h[N];
    //ne数组存储的是这条边的前驱的点指向的另一条边
    void add(int a,int b,int c){
    e[++cnt]=b; //e数组存储的是这一条边的后继，即指向的边
    w[cnt]=c; //w数组存储的时这一条边的长度
    ne[cnt]=h[a]; //ne数组指向原先这条边的前驱的点出发的第一条边，
    h[a]=cnt; //h数组存储的是从这个点出发的第一条边
}

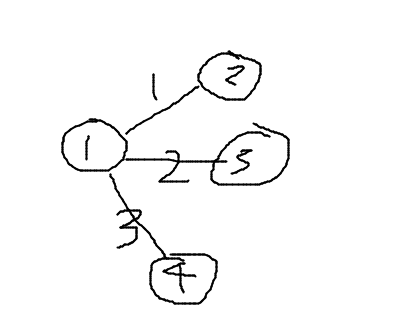
再放一张图便于理解：

从第一个点开始建图

e[1]=2，即指1这条边的后继（指向的点）是2

w[1]=1，1这条边的长度为1

ne[1]=h[1]，此时h[1]=0所以ne[1]=0即这是这个点的最后一条边,这条边没有对应的下一条边。

h[1]=1，即指1这个点出发的第一条边为1

接下来add(1,3,2)

e[2]=3，2这条边的后继为3

w[2]=2，2这条边的长度是2

ne[2]=h[1] ，此时h[1]=1，所以ne[1]=1,即这条边的下一条边是1。

h[1]=2 ，即1这个点出发的第一条边为2。

以此类推，使得图以一种邻接表的方式存储下来，空间较小，且找对应边较快。

Dijkstra算法

模板题：洛谷P4779

#include <iostream>
#include <stdio.h>
#include <algorithm>
#include <cstring>
#include <queue>
#define PII pair<int,int>
#define ull unsigned long long

using namespace std;

const int N=2e5+10;

int n,m,s,a,b,c,cnt;
int h[N],ne[N],e[N],w[N];
ull d[N];
bool vis[N];
priority_queue<PII,vector<PII>,greater<PII> >q;

void add(int a,int b,int c){
	e[++cnt]=b;
	w[cnt]=c;
	ne[cnt]=h[a];
	h[a]=cnt;
}
void dij(){
	memset(d,0x3f,sizeof d);
	d[s]=0;
	q.push({0,s});
	while(!q.empty()){
		PII x=q.top();
		q.pop();
		int dis=x.first,ver=x.second;
		if(vis[ver]) continue;
		vis[ver]=1;
		for(int i=h[ver];i;i=ne[i]){
			int j=e[i];
			if(d[j]>dis+w[i]){
				d[j]=dis+w[i];
				q.push({d[j],j});
			}
		}
	}
}
int main(){
	scanf("%d%d%d",&n,&m,&s);
	for(int i=1;i<=m;i++){
		scanf("%d%d%d",&a,&b,&c);
		add(a,b,c);
	}
	dij();
	for(int i=1;i<=n;i++){
		printf("%lld ",d[i]);
	}
}

扩展：洛谷P1629

spfa

#include <iostream>
#include <stdio.h>
#include <algorithm>
#include <cstring>
#include <queue>

#define NN N<<1

using namespace std;
const int N=1e5+10;

int n,m,h[N],e[NN],ne[NN],w[NN],d[N],f[N],t,cnt,a,b,c;
bool v[N];

void add(int a,int b,int c){
	e[++cnt]=b;
	ne[cnt]=h[a];
	h[a]=cnt;
	w[cnt]=c;
}
bool spfa(){
	memset(d,0x3f,sizeof d);
	memset(v,0,sizeof v);
	memset(f,0,sizeof f);
	queue<int>q;
	q.push(1);
	d[1]=0;
	while(q.size()){
		int x=q.front();
		q.pop();
		v[x]=0;
		for(int i=h[x];i;i=ne[i]){
			int y=e[i],z=w[i];
			if(d[y]>d[x]+z){
				d[y]=d[x]+z;
				f[y]=f[x]+1;
				if(f[y]>=n) return true;
				if(!v[y]) q.push(y),v[y]=1;
			}
		}
	}
	return false;
}
int main(){
	scanf("%d",&t);
	while(t--){
		memset(h,0,sizeof h);
		memset(e,0,sizeof e);
		memset(ne,0,sizeof ne);
		cnt=0;
		scanf("%d%d",&n,&m);
		for(int i=1;i<=m;i++){
			scanf("%d%d%d",&a,&b,&c);
			add(a,b,c);
			if(c>=0) add(b,a,c);
		}
		if(spfa()) printf("YES\n");
		else printf("NO\n");
	}
}