前言
训练的时候打了一场NWERC2021,虽然里面的题目之前学长拉过了,但是我竟然在看赛时过方法的情况下还是不会。并且不知道到底是因为精度还是哪里处理错了WA了20发,十分痛心。遂决定随手把我会的最基础最基础的东西记录下来。
在namomo winter camp的时候,是逆命队的fstqwq教我们计算几何的。当时他说“今天的目标是知道什么是叉积”。正好,我只学会了叉积。
所以,我们的目的也是:学会点积和叉积。
下面的代码很多都是借鉴的fstqwq的ppt里的板子。
计算几何简介
利用计算机建立数学模型解决几何问题。——摘抄自oiwiki
计算几何引入
都说了是基础了,我毕竟也不会什么科技,所以不如干脆从头头头头头开始讲。
什么是几何呢? 本来想多抄点定义的,但是感觉抄的多了好像没什么意思。
按照我个人的理解,总而言之就是几何图形。例如,三角形,正方形。那么要怎么让计算机对于几何图形进行运算呢?这里就要用到我们在中学数学里的“通解”了,那就是建系。
建系就是建立直角坐标系。
几何图形是由点和线构成的,两点一线。在坐标系则有点和向量来快速确定点与点之间的关系。
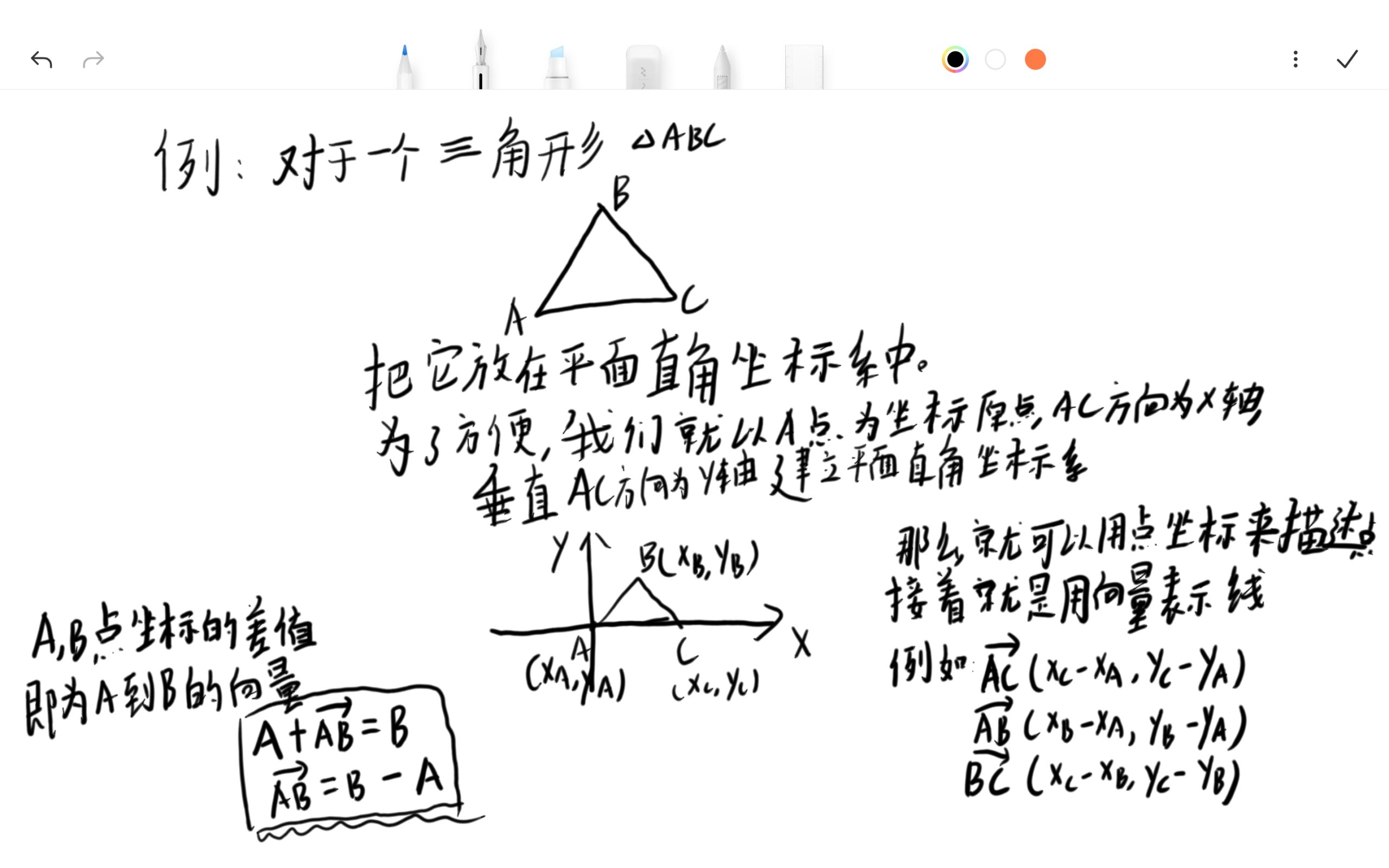
例如:
转换成代码语言:
typedef double LD; //可以用来避免卡精度的时候要一个个的修改变量类型
struct point{
LD x,y;
point operator + (const point &a) const {
return {x+a.x,y+a.y};
}
point operator - (const point &a) const {
return {x-a.x,y-a.y};
}
};
struct line{
point s,t;
};
point A(0,0),C(2,0);//点
line AC(A,C);//线
point Delta=C-A;//向量那么上面这些应该是最基础最基础的部分了。
其实应该还有线围绕着点的旋转应该也算是基础。但是我不会。
那么接下来就讲点积和叉积吧。
点积和叉积
什么是点积
学过中学数学的都知道,向量与向量相乘的结果是这样的
$$\vec{A} \times \vec{B} = |A| \times |B| \times cos\theta $$
这个在计算机几何里就叫做叉积。
$$dot = |A||B|cos \theta $$
LD dot (const point &a,const point &b){
return a.x*b.x+a.y*b.y;
}什么是点积
在我学高中数学的时候,在二级公式里面找到一个超级方便的求三角形面积的方法。在讲其中的两条边用向量表示后,即可用向量三角形的面积公式快速求出面积,不需要用任何复杂的方式了。(可以说直接秒杀)
$$S=\frac{1}{2}|A||B|sin \theta =\frac{1}{2}|x_{1}y_{2}-x_{2}y_{1}|$$
叉积可以简单的看成是两个向量围成的三角形面积的两倍。
$$det=|A||B|sin\theta=x_{1}y_{2}-x_{2}y_{1}$$
LD det (const point &a,const point &b){
return a.x*b.y-b.x*a.y;
}
]
那么点积和叉积的公式就都讲完了,这两者具体要怎么用呢?
$$dot = |A||B|cos \theta $$
$$det=|A||B|sin\theta$$
显然,我们可以运用这个来帮助我们求向量间的夹角。
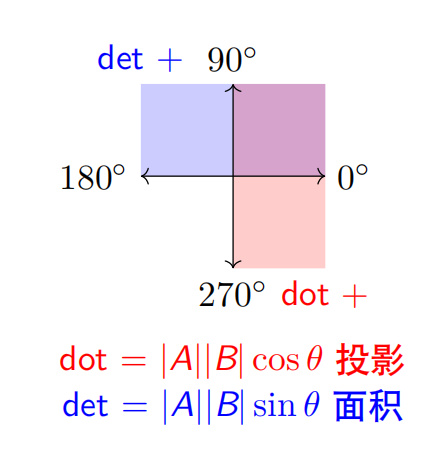
那么同时,我们也可以用点积和叉积作为工具,在不计算角度的情况下判断夹角的象限。
如图所示,我们可以通过计算出的$cos\theta$和$sin\theta$的正负来判断出夹角处于哪一象限(角度的大小位于哪个范围)。
换句话讲,我们可以用计算机来把位于一个向量两侧的向量隔离开。同时,也可以用来判断向量之间是否平行。
如何判断等于
差点忘记了,写计算几何题还有一个最重要的一点:
由于浮点数的表示形式的问题,经常会有误差,或者说精度不对。
所以我们有时需要将两个相差很小的数看成是相等的(通常是10的负6次及以上,具体要根据题目的限制,有时题目的计算带有平方或者根号时,对于精度的要求就更大了)
const LD eps=1e-8;
int sgn(LD x){
return x>eps?1:(x<-eps?-1:0);
}在这里的话我们只需要判断两个数的差代入到这个函数里的结果是不是0即可,如果是0的话表示相等。
例题
Balloon Darts

就是找到三条线,把所有的点都包括进去。
首先,我们要怎么判断点在直线上呢?
这里就用到了叉积。叉积可以看成是向量间围成的三角形的面积的一半,也可以就关注公式里面的$sin\theta$,注意到把点与直线上任何一个点连起来组成一条线,如果这两条线夹角为0,或者说组成的三角形面积为0,那么显然,该点就在直线上。
接下来就是怎么找直线了。
在这里有个结论:
假设k条直线可以穿过全部点,那么在k+1个点中至少有两点在同一条直线上。
解释:显然的,最坏情况是k个点中没有两个在同一直线上,那么再加1个点,一定会与这k个点中的一个组成一条答案中的直线。
那么这题就结束了。
Flatland Olympics



那么接下来要处理的就是把点按照角度排序。
我赛时由于计算几何没学好所以打算通过点积除以两条线的长度比较$cos\theta$的大小来进行角的大小的排序。
但是,你知道的,有除法就有精度问题,当然也可以改成将左右两边式子的某些值交换用乘法比较,。但是由于求长度时有着根号(会掉精度),并且把根号去掉后(平方)四次相乘的数据已经爆long long了,并且这种方法有点小抽象。或者说我写的很抽象。(太菜了)所以赛时WA了20发也不知道哪里有问题。所以这种方法肯定不好。
实际上,这里我们依然可以使用叉积的方式来给角排序。我们在上面讨论过,叉积的正负可以用来判断一个向量在另一个向量的哪一侧。那么我们只需要将a<b定义为b在a的某一侧即可。每个相邻的都是如此,那么最后找这个规则排序后的数组也是有序的。
需要注意的是,我们要将与跑道在不同侧的点分开考虑,这里使用叉积的正负将他们分开。同时,要把与跑道在同一直线(叉积为0)的分开考虑,这样子不容易错。在这条直线上两侧(点积正负)的点单独考虑。
这题就结束了。
总结
那么祝愿大家都能学会点积和叉积。
本人才疏学浅,只会这么一点东西。希望有点用。如果有遗漏或者错误之处的话,十分抱歉。
祝好。